📚 Personal Review on Spoof Surface Plasmon Polaritons (SSPPs) and Its Applications in Flexible Electronics
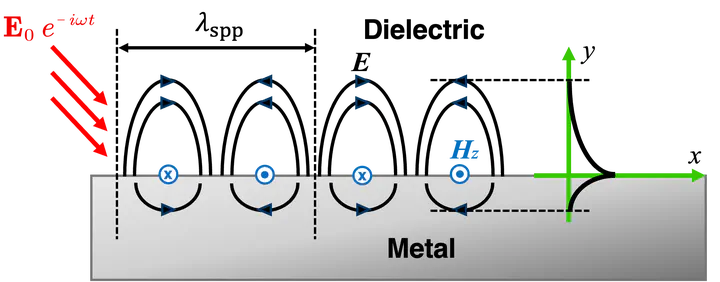
What is Surface Plasmon Polaritons (SPPs)?
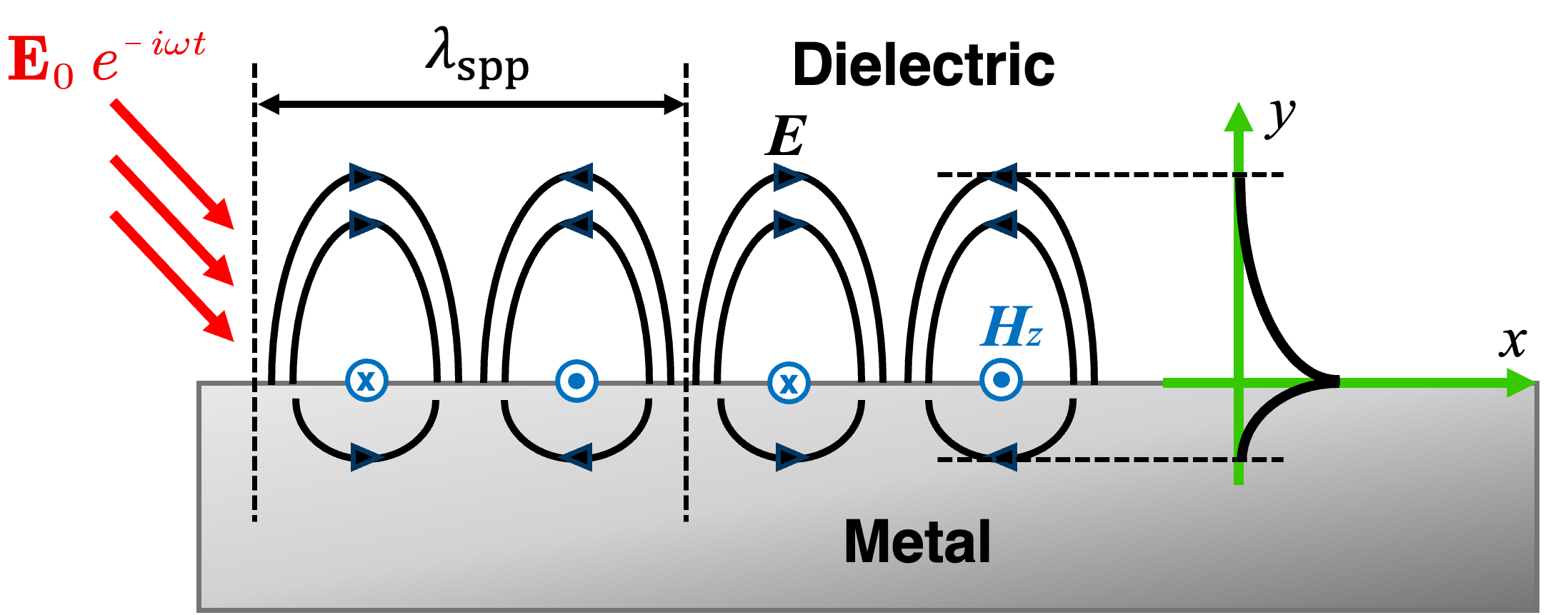
Surface plasmons are special electromagnetic waves that travel along the interface between a metal and a dielectric (insulator). Unlike ordinary electromagnetic waves, these surface-bound waves strongly interact with electrons at the metal surface, creating oscillations that can propagate along the interface without radiating away. As shown in the figure above, the induced Electromagnetic (EM) wave excites the free electrons in the metal, and creates a strong coupling between the EM wave and the electron oscillations. And this coupling mode can be transported along the metal-dielectric interface, leading to a surface plasmon polariton (SPP) wave.
Drude-Lorentz Model
To understand the behavior of SPPs, it is essential to introduce the Drude-Lorentz model. The Drude–Lorentz model describes the permittivity of materials at high frequency. It is a classical description used to understand how materials, particularly metals and dielectrics, respond to electromagnetic waves.
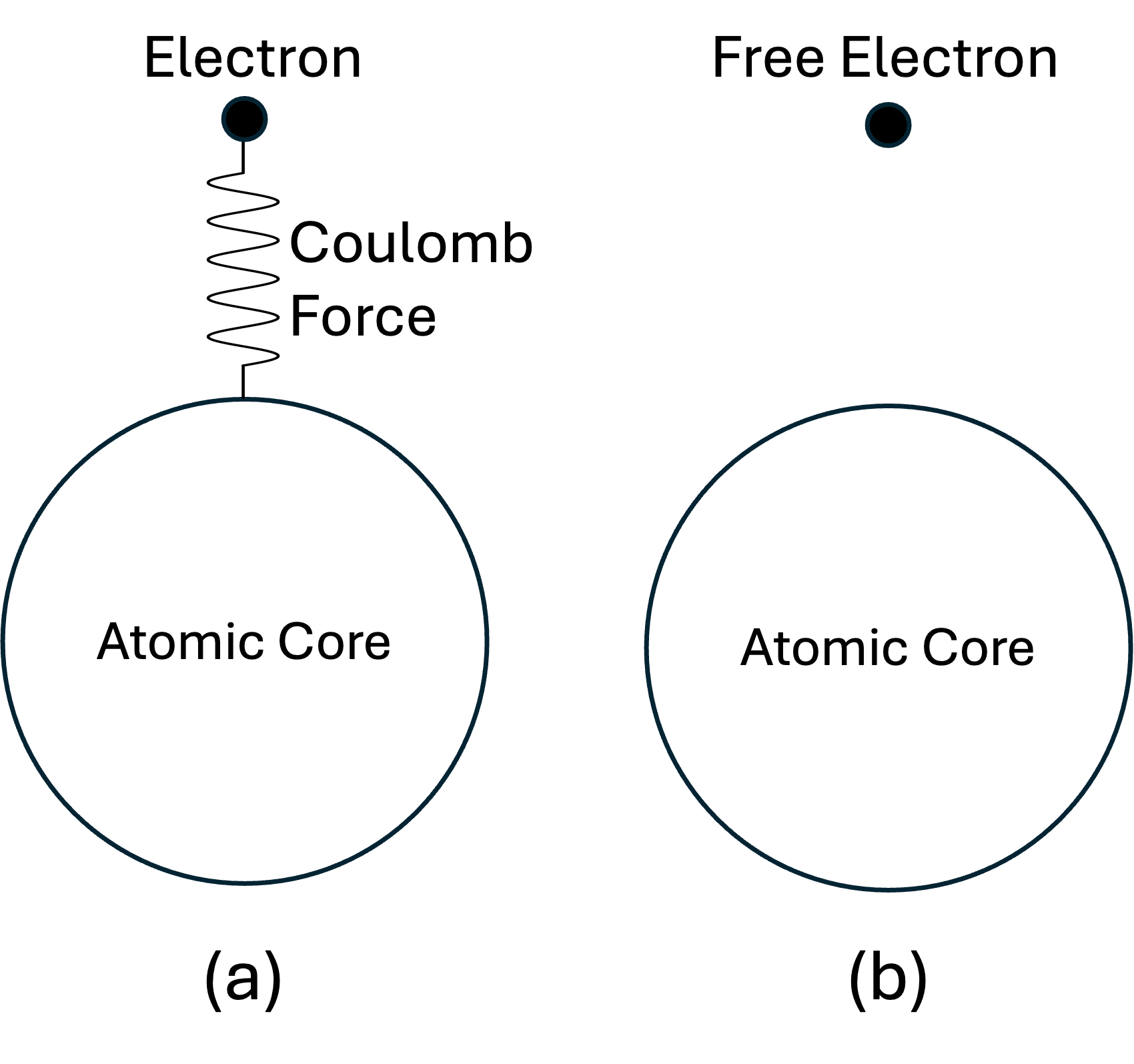
- The positively charged atomic cores in a metal are surrounded by an electron gas. The core is much heavier than the electrons, and the strong coulomb force between the core and the electrons is described by a harmonic potential.
- When an external electric field 𝐄0 𝑒−𝑖𝜔𝑡 is applied, the electrons are displaced from their equilibrium positions. The forced oscillation of the electrons is described by the equation: $$ m_e \,\frac{d^2 \mathbf{r}}{dt^2} \;+\; \gamma\,m_e \,\frac{d \mathbf{r}}{dt} \;+\; K \,\mathbf{r} \;=\; -\,e\,\mathbf{E}_0\,e^{-i\omega t} $$
Where:
- \(m_e\) is the mass of the electron.
- \(\gamma\) is the damping coefficient, which accounts for the energy loss due to collisions and other dissipative processes.
- \(K\) is the spring constant of the harmonic potential, which is related to the stiffness of the restoring force that brings the electrons back to their equilibrium positions.
- \(e\) is the charge of the electron.
- \(\mathbf{E}_0 e^{-i\omega t}\) is the applied electric field, where \(\mathbf{E}_0\) is the amplitude of the electric field and \(\omega\) is the angular frequency of the oscillation.
- \(\mathbf{r}\) is the displacement of the electrons from their equilibrium positions.
- The electrons will eventually oscillate at the same frequency as the external field. The solution should be in the form $\mathbf{r}=\mathbf{r_0}e^{-i\omega t}$. The final displacement of the electrons is given by the equation: $$ \mathbf{r}=\frac{e/m_e}{\omega_0^2-\omega^2-i\gamma\omega}\mathbf{E_0}e^{-i\omega t} $$
If we apply the solution of displacement of the electrons to $\mathbf{P}=N_a~e\mathbf{r}$ we obtain the polarization of the medium per unit volume, it is given by:
$$ \mathbf{P}=\frac{N_ae^2/m_e}{\omega_0^2-\omega^2-i\gamma\omega}\mathbf{E_0}e^{-i\omega t}=\frac{ \tilde{\omega}_p^2}{\omega_0^2-\omega^2-i\gamma\omega}\mathbf{E_0}e^{-i\omega t}=\chi\varepsilon_0\mathbf{E} $$Where:
- $N_a$ is the number density of atoms.
- $\tilde{\omega}_p^2=\frac{N_ae^2}{m_e}$ is used to simplify the expression.
- $\chi$ is the susceptibility of the medium.
Finally, the expression for relative permittivity $\varepsilon_r$ can be obtained by substituting it into the equation for the electric displacement field $\varepsilon_r=1+\chi$, as shown in the following equation:
$$ \varepsilon_r=\frac{\varepsilon}{\varepsilon_0}=1+\frac{ \tilde{\omega}_p^2/\varepsilon_0}{\omega_0^2-\omega^2-i\gamma\omega}=1+\frac{\omega_p^2}{\omega_0^2-\omega^2-i\gamma\omega} $$Here $\omega_p^2=\frac{N_ae^2}{m_e\varepsilon_0}$ represents the plasma frequency, indicating the characteristic frequency at which free electrons in the metal collectively oscillate. The plasma frequency is a key parameter in determining the optical properties of metals, as it determines the frequency range over which the metal behaves as a good conductor. The value of plasma frequency $\omega_p$ and damping factors $\gamma$ for some noble metals are shown in the table below:
| Metal | Plasma Frequency ($10^{15}Hz$) | Damping Factor ($10^{12}Hz$) |
|---|---|---|
| Silver | 2.18 | 4.35 |
| Gold | 2.18 | 6.46 |
| Copper | 1.91 | 8.34 |
| Aluminum | 3.57 | 19.79 |
| Platinum | 1.24 | 16.73 |
In practice, the electrons in metals are regarded as free electrons, which means the spring factor $K$ is negligible. The model is further simplified as the Drude model without the Lorentz term. The relative permittivity of the metal can be simplified as:
$$ \varepsilon_r(\omega)=1-\frac{\omega_p^2}{\omega^2+\gamma^2}+i\frac{\gamma\omega_p^2}{\omega(\omega^2+\gamma^2)} $$In the near-infrared (NIR) and visible ranges, the relative permittivity of metals can be further simplified as:
$$ \varepsilon_r(\omega)=1-\frac{\omega_p^2}{\omega^2} $$In the near-infrared (NIR) and visible (VIS) range, the frequency is about $10^{14} Hz$, and the permittivity in this range is naturally negative. This negative permittivity is the key to the generation of SPPs.
Why it only works at the surface?
To be continued…